Transient (Lumped Capacitance) Calculator

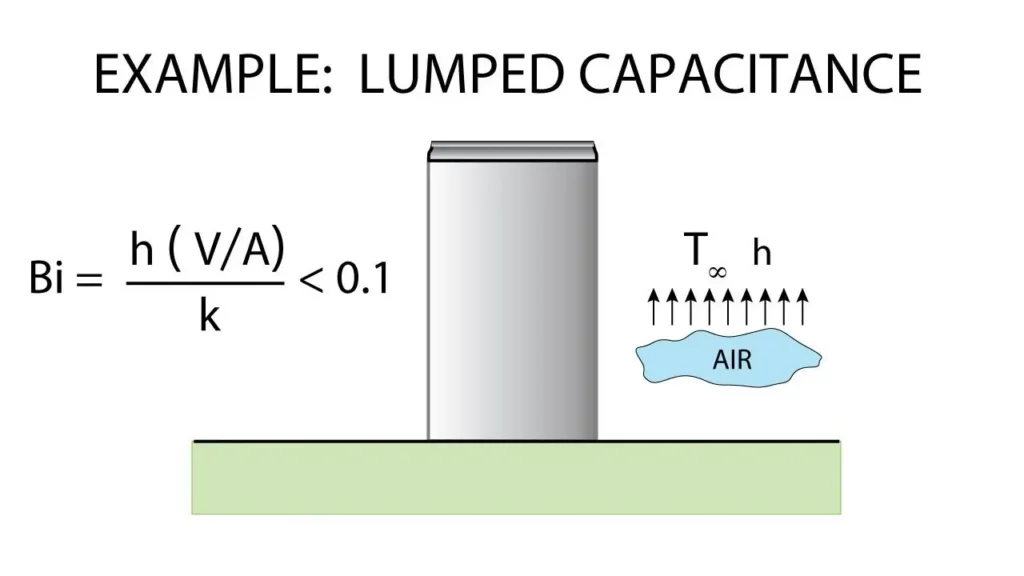
For systems where Biot number (Bi) < 0.1

Configuration

Object & Environment Properties

Calculate Time History

s

Note: This calculator assumes the Lumped Capacitance Method is valid (typically when Biot number, Bi = hLc/k, is less than 0.1). The characteristic length Lc is Volume/Area. Thermal conductivity (k) is not an input here, so ensure this condition is met for your material and conditions.

Formulas used:

  • Time Constant: τ = (m · c) / (h · A) or τ = (ρ · V · c) / (h · A)
  • Temperature: T(t) = T∞ + (T0 – T∞) · e(-t/τ)
  • Time to Target Temp: t = -τ · ln[ (Ttarget – T∞) / (T0 – T∞) ]

A Transient (Lumped Capacitance) Calculator calculates the temperature of an object over time when it’s being heated or cooled by a heat transfer process, assuming the temperature is uniform throughout the object. This simplification, called the lumped thermal capacity model, is valid when the Biot number is small, meaning internal conduction resistance is much larger than external convection resistance. It’s a useful tool for analyzing transient heat transfer scenarios.

Transient (Lumped Capacitance) Calculator

Here’s a breakdown of what the calculator does:

1. Inputs:

  • Object Properties: Volume, mass, density, specific heat capacity.
  • Heat Transfer Conditions: Surface area, convective heat transfer coefficient (h), surrounding temperature (T∞).
  • Initial Temperature: The starting temperature of the object.
  • Time: The time period you want to analyze. 

2. Calculations:

  • Biot Number: Calculates the ratio of internal conduction resistance to external convection resistance, which determines the validity of the lumped capacitance assumption. 
  • Time Constant: Determines how quickly the object’s temperature changes. 
  • Temperature: Calculates the temperature of the object at different times during the heat transfer process. 

3. Outputs:

  • Temperature Profile: A graph or table showing the temperature of the object as a function of time. 
  • Analysis of Biot Number: Whether the lumped capacitance model is valid for the given conditions. 

In essence, the calculator simplifies the complex transient heat transfer equations by assuming a uniform temperature throughout the object and solving for the temperature change over time.